複素関数のカラフルな可視化をPython・JavaScriptで実装する
これは「日曜数学 Advent Calendar 2018」4日目の記事です。
みなさんレベルが高くて恐縮ですが、この記事では気軽に目で見て楽しめる内容を紹介させていただきます。 adventar.org
なお、複素関数の可視化に関連して、以下のような記事も書いています。 ぜひ併せてご覧ください。
1. 複素関数の可視化について
初めて複素数を学ぶ高校生が の実体を想像できずに苦労するというのはたまに聞く話ですが、複素関数ともなればさらにイメージしにくいのではないでしょうか。「普通の」関数ならグラフを描画して性質を考えることもできますが、複素関数の場合はそうもいきません。
そこで、この記事ではDomain Coloring(定義域の着色)*1という手法によって複素関数を可視化してみます。
まずはふつうの実数値関数のグラフを考え、関数の可視化がどのような発想に基づくものであるかを明らかにするところから始めましょう。
1.1. 実数値関数の可視化方法
実関数 を可視化したい場合を考えます。一般的に使われるのは折れ線グラフですが、その考え方は、入力と出力に一次元ずつ(
軸・
軸)空間を割り振り、入出力の関係性
を二次元平面に描画するというものです。紙やディスプレイは二次元なのでこれは上手くいきますね。

ちょっと複雑になって のような二変数関数を可視化するときも同様で、入力に二次元・出力に高さの一次元を割り振り、入出力の関係性
を三次元空間上の曲面として描画することになります。ただし、三次元空間を二次元平面に投影して描画する必要が生じてきます。

1.2. 複素関数の問題
では、複素関数の場合は? 複素数と複素数の入出力関係を可視化したいのですが、入出力それぞれに実部と虚部があることにより、グラフの考え方に基づいて可視化しようとすると4次元空間が必要になってしまいます。
1.3. Domain Coloringによる解決
先述の問題を解決して二次元平面に可視化する方法がDomain Coloring (定義域の着色)です*2。
核となるアイディアは出力値を表現するために空間ではなく色を用いることで、可視化したい複素関数を として、以下のようにします:
複素数
が複素関数
によって
に移されるとする。 このとき、
の偏角
に基づいて色相を定め、複素数平面の点
を(
でないことに注意 )その色で塗る
図にすると以下の通りです。

より具体的には、以下のような手順によって平面を塗り潰していきます。
1.1.の説明に基づいてこの手法を捉え直すと、入力 の
に二次元を割り振るまでは1.1.同様ですが、出力は極座標変換 (
)を介して色に変換し、定義域の二次元平面を塗りつぶしているということになりますね。
より直感的に(雑に)言い換えると、Domain Coloringとは、虹色に塗り分けられた複素数平面(先ほどの図の右側)が複素関数によって歪められる様子を視覚化する手法*3と言えるでしょう。
2. Pythonによる実装
2.1. Pythonと複素数
z1 = 2 + 3j
print(z1)
# -> (2+3j)
print(type(z1))
# -> <class 'complex'>
また、Numpyの多くの関数も複素数をサポートしています。
import numpy as np
print(np.exp(2 + 3j))
# -> (-7.3151100949+1.04274365624j)
2.2. 実装
様々な複素関数に対して可視化を行えるようにしたいので、複素関数を引数として描画を実行する高階関数を定義するのがよいでしょう。以下のように数行で実装することができます。なお、この実装ではによる明度の調整は行わず、偏角に基づく色分けのみ行なっていることに注意してください。
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
def plot_complex(complex_func):
""" 複素関数を受けてDomain Coloringを行う関数 """
x, y = np.meshgrid(np.linspace(-4, 4, 400), np.linspace(-4, 4, 400))
z = x + y*1j
angles = (np.angle(complex_func(z)) + 2*np.pi) % (2*np.pi) # pi関連は、偏角をx軸基準で時計回りにするための調整
im = plt.imshow(angles, origin="lower", cmap="hsv") # origin="lower": y軸を上向きにする
plt.axis('off') # 軸の数値を非表示
plt.colorbar(im, fraction=0.046, pad=0.04) # colorbarの高さを画像に合わせている
以下のように関数を渡すことで可視化を実行することができます。
plot_complex(np.sin)

Scipyを利用すれば特殊な関数も呼び出せます。例えばディガンマ関数なら以下のようにします。
from scipy import special
plot_complex(plot_complex(special.digamma))
実装や実行結果はJupyter Notebookに公開しています。
3. JavaScriptによる実装
ソースコード全体は以下に置いています。
visualization/Complex.jsx at material · sw1227/visualization · GitHub
まずは偏角を計算して0-1の間に正規化する関数を定義しておきます。
// (x, y) => Argument(angle) [-PI, +PI] => [0, 2*PI] => [0, 1]
export function normalizedArg(x, y) {
return (math.atan2(y, x) + 2*Math.PI) % (2*Math.PI) / (2*Math.PI);
}
そして、Pythonの時と同様にDomain Coloringの処理を実装します。ここで、funcという引数には可視化したい複素関数(math.exp, math.gammaなど)を渡し、methodには先ほどのnormalizedArgという関数を渡します。複素数・複素関数はmath.jsというライブラリを用いて扱っています。
computeData = (func, method) => {
const resolution = 800; // # of pixels
const range = 4; // drawing range
const data = d3.cross(
d3.range(-range, range, 2*range/resolution).reverse(),
d3.range(-range, range, 2*range/resolution)
).map(coord => {
const transformed = func.function(math.complex(...coord.reverse()));
return method.function(...math.complex(transformed).toVector());
});
return data;
}
この返り値を二次元上に可視化すればいいのですが、Pythonのmatplotlib.imshow()という便利な関数が使えないので、下記のQiitaに書いた方法を用います。
Pythonのimshow()と同様の可視化をJavaScriptで行う - Qiita
上記記事の「Reactを使う場合」に記したImshowコンポーネントを使い、
<Imshow data={this.state.data} interpolate={this.state.interpolate.scale}/>
ようにデータを渡します。ここで、this.state.dataにはcomputeData()の返り値が、this.state.interpolate.scaleは0-1の値を色に変換するカラースケール関数(今回はd3.interpolateSinebow)が入っているものと考えてください。
このように実装した結果は以下のURLにデプロイしました。ドロップダウンで「Color Scale: Rainbow」「Method: Argument」とするとこの記事に書いた通りの可視化になります。ぜひ触ってみてください。
https://sw1227.github.io/#/complex
4. 代表的な複素関数での実行例
恒等写像
単に複素数平面を偏角に応じて色分けしたカラーピッカーのような画像になります。
なお、逆数をとる という関数も、偏角に影響を及ぼさないため同様の画像になります。

平方根
赤系の半分の色のみ表示されていますね。 実は、Riemann面を可視化(手法や実装方法は後日書く予定)すると以下のように二重に丸め込まれている*4ことが分かり、納得感があります。

指数関数
縦軸(虚部)のみに依存していることが分かります。これは、 として
となることからも納得できるかと思います。

対数関数

sin関数

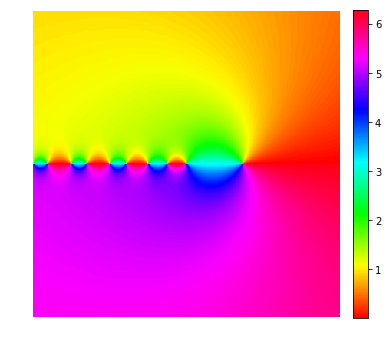
ガンマ関数

5. 今後の課題など
今回はDomain Coloringに基づく可視化を行いましたが、他にも以下のような方法が考えられます。
実装自体はできているので、近いうちに記す予定です。 また、複素関数の性質をこれらの可視化に基づいて理解する例が提示できれば良いなと考えています。 大学の複素解析で勉強するような特異点・留数定理・ローラン展開なども、こうした可視化と見比べながら理解していくと興味深いのではないでしょうか。
以上
